「平滑上期」什么是指数平滑法（指数平滑法的逻辑和初始化详解）

今天，神州网给大家普及下关于「平滑上期」什么是指数平滑法（指数平滑法的逻辑和初始化详解）的知识。

让我们拿踢足球打比方，来进一步理解指数平滑法的逻辑。

如图 1，预测就如防守方，下一步跑到哪里，取决于（1）现在球落到什么地方，即上期的实际值；（2）现在自己的位置，即上期的预测值——防守者是按照自己的预测行事，他现在的落点就是上期的预测值。

或许有人会问，所有的预测都是错的，为什么还要考虑以前的预测，错上加错？这貌似有悖常理，其实不然。其一，我们现在的落点不是上一步实际发生的，而是上一步预测要发生的（我们是在按预测行事）。所以，下一步的出发点不是上次的实际值，而是上一次的预测。也就是说，两个预测之间天然是有联系的。其二，上期的预测不是简单的预测，而是以前需求历史的结晶，就如前面公式中所示，正是通过上期的预测，我们得以把所有的需求历史考虑在内，包含了很多历史信息。

图1：指数平滑法的逻辑就如防守队员

下一步行动，也就是预测，介于两个极端：一个极端是“我行我素”，严格按照原来的计划（上期预测），实际上是拿上期预测作为下一步的预测（平滑系数α为0）；另一个极端是“步步紧逼”，上一次球落到什么地方，就赶到什么地方，实际上是拿上期实际值作为下一步的预测（平滑系数α为1）。

“我行我素”是以不变应万变，风险是可能没法及时响应变化了的局势；“步步紧逼”看上去很积极，实际上是跟着球跑，永远慢一步，永远也抢不到球——看上去让人觉得很“响应”，其实是典型的被动反应，给供应链导入频繁的变动，导致产能利用率低，运营成本高，也注定永远没法超前。

如果要超前，就得预判，就得按照一定的战略行事，沿着特定的路径前行，注定不会亦步亦趋地“紧贴”需求，在灵敏度上受限，牺牲短期利益来获取长期利益，在企业追求无限响应的今天，往往也更不受欢迎。

在实际操作中，综合考虑已经发生的，辅之以对未来的预判，目标是让防守者尽可能地接近球（最小化预测误差），最大化抢到球的概率（服务水平，有货率等），平滑系数α会在这两个极端之间取值。寻找最佳的平滑系数α，以提高预测的准确度，就是指数平滑法的择优过程，我们稍后继续。

对于指数平滑法来说，我们有个初始化问题，也就是说，为了让它运作起来，我们得首先做的一些事，包括初始预测的选择和模型的“预热”。

先说初始预测。指数平滑法下，预测是基于上期实际值和上期预测值。上期实际值我们有，但我们往往没有上期的预测值。我们有几种方式来设定初始预测：一种方式是假定上期预测就等于上期实际值；一种方式是用别的方法，比如移动平均法计算一个预测；还有一种方式，就是随便填个数字进去，比如0。

有趣的是，经过几次迭代后，你会发现，初始预测值的影响很快就变得非常有限，直至衰减到没有。比如在图 2中，三种预测都用简单指数平滑法，但初始预测各不相同：预测1的初始值采用上期实际值，预测2的初始值非常接近1到5周的平均值，预测3就随便假设为0。你发现，刚开始的时候，预测值的差异很大，但经过几次迭代后，三种情况下的预测值就基本一样了。而对于第22周的预测，也就是我们真正需要的预测，预测的初始值就根本没有任何影响。

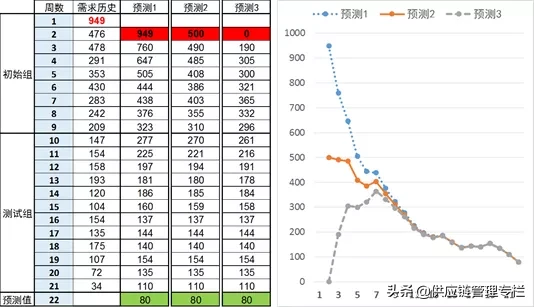
图2：指数平滑法的初始化和“预热”

为什么呢？这跟指数平滑法下，历史数据的权重按照几何级数衰减有关。就拿图 2中的例子来说，平滑系数α是0.4，参照前文的公式，这意味着在第3周的预测中，初始预测值的权重为(1-0.4)=0.6；到了第4周，初始预测的权重就成了(1-0.4)2=0.36；到了第5周，这一权重成为(1-0.4)3=0.216。依次类推，用不了多久，你会发现初始预测的影响就基本衰减到了0。

但是，在刚开始的几期，初始预测的影响还是很显著的。这就是为什么指数平滑法要有个“预热”的过程，不管是这里谈的简单指数平滑法，还是后面要谈到的霍尔特和霍尔特—温特模型，都是如此。这跟厂房投产前的“试运行”类似：用一段的历史数据来建立模型（“初始组”），等“预热”完成后，就进入正式的“测试组”，围绕测试组的数据，我们统计预测的准确度，比较不同的平滑系数的优劣，选择最优的平滑系数α。

在一些预测方面的经典著述中，一般用最初的9个数据点作为指数平滑法的初始数据[1]。如果是按照季度汇总，这大致就是2年的数据；如果按照周来汇总，大致就是2个月的数据。

初始化就如正式比赛前的热身，或者设备投入正式运营前的试车，在试车走合的过程中，我们可能调整有些参数，让设备处于更好的状态（优化）。对于预测模型来说，这种调整更多的是自动调整——好的预测模型往往有一定的“自适应性”，初始化就是指数平滑法的“自适应”过程。

对于测试组，顺便补充几句。指数平滑法之所以有“测试组”，是因为平滑系数α的择优问题。比如在图 2的例子中，我们用第10到21期的数据作为测试组，共12个数据点，针对不同的平滑系数α，我们复盘这12期的预测，跟每期的实际值比较，得到每期的误差，然后求得12期的平均误差，比如均方差，作为平滑系数α择优的依据。

要注意，“预热”的数据不能用于测试模型准确度，“测试”的数据不能用于“预热”，避免了“既做裁判，又做球员”的情况，这有点像立法和执法要分离的一样。

那么，测试组究竟该有多少数据点？我没有看到具体的研究。在我参考的一些书中，比如Makridakis 等人的著作[2]，经常看到用12期的数据。我想这有几个原因：其一，这些研究中，时间单元一般是月，12个月正好是完整的一年，覆盖到每个月，降低了潜在的季节性、周期性、趋势等影响。其二，十来个数据点，不算多，但也不算太少，在数理统计上有一定的可靠性。

一般来说，测试组的数据点越多越好；但在实践中，我们往往没有那么多的数据点。比如就图 2的例子来说，产品是快消品，生命周期往往就只有几个月，按周拆分的话，也没有多少个数据点。我在做分析的时候，会力求用13周或更多数据点来测试，这样我们覆盖一个完整的季度。当然，这只是个人实践，仅供参考。